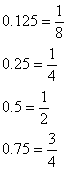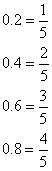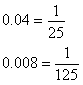数学のコツのまとめ（考え方・勉強法・解き方）

分からない問題（難問）を解くコツ

　リンクをクリックするとコツの内容が表示されます。

考え抜く

　数学は、全ての教科の中で１番「考える力」が重要な科目です。

　そして、「考える力」はどんな頭のいい人も教えることができません。

　「考える力」は自分の頭で考えることでしか身につかないものなのです。

　「考えるのをすぐあきらめる」勉強ではなく、

　「考え抜く」勉強をしていきましょう。

計算力を身につける。

　計算というのはできて当たり前の内容で、難しい内容ではないのですが、早く正確に計算するということになると、それができる子はなかなかいません。

　複雑な計算になると、計算間違いをしてしまうお子様が多いです。

　計算とは「読み・書き・そろばん」のそろばんに該当しますが、全ての科目の基礎になる部分です。

　計算は「早く」「正しく」が大切です。

　計算に時間がかかってしまったり、計算まちがいが多ければ、それがそのままテストの時間の配分や得点にはねかえってきます。

　ではどうすれば、「早く」「正しく」計算できるようになるのでしょうか？

　それは、どうすれば簡単に計算できるか考えながら計算し、計算を簡単にするための工夫をすることです。

　難しい計算でも、式の変形などして計算を簡単にするための工夫をすれば、「早く」「正しく」計算できます。

　計算を何も考えず計算するのではなく、常日頃、

　もっと簡単に計算するためにはどうすればいいか？

　と考え計算を簡単にするための工夫を考えながら計算をしていくことが重要です。

　そうすれば、難しい計算に出会っても、ここはこういうふうに工夫すれば簡単に計算できるというのが無意識に分かってくるようになります。　

　できてあたりまえのことかもしれませんが、だからこそ「早く」「正しく」計算することのできる計算力を身につけましょう。

公式を「覚える」のではなく「理解する」

　数学の勉強で大切なことは

　公式を覚えるのではなく、理解することです。

　そしてその際、基礎的な内容は具体的に、高度な内容は実際に数学的に証明して理解することです。

　覚えても、理解しても同じではないかと思われる方がいらっしゃるかもしれませんが、ただ意味も理由も分からず覚えている内容というのは応用できないのです。

　全ての科目に言えることですが、理解した内容でなければ応用できません。

　公式は覚えるものという認識をまず捨て、時間がかかってもいいので、基礎的な内容は具体的に、高度な内容は数学的に証明して理解していきましょう。

数学特有の用語の意味を理解する。

　算数・数学には、算数・数学特有の用語がよく出てきますが用語の意味・定義を、ただ文字の羅列（られつ）として覚えたり、漠然と理解するのではなく正確に理解することが大切です。

　なぜなら、用語の意味を正しく理解していないと、その用語を使って説明している内容を理解することができないからです。

　また、問題を解く場合において、用語の正しい意味・定義が分からなかったら問題を誤って理解することになりますし、用語の正しい意味・定義が問題を解くために必要な条件だったりします。

　算数・数学においては、用語の意味・定義がとても大切です。

　用語の意味・定義を、正確に理解していきましょう。

解法パターンを理解する。

　テストによく出る問題のパターンというものはある程度決まっています。そして、それらの問題も、もちろん基礎を応用すれば解くことができるのですが、その場合考えるのに結構時間がかかってしまいます。

　普段の勉強では、基礎を応用してじっくり考えればいいのですが、テスト等の限られた時間では、よく出題される問題の解法を理解しておいた方が、少ない時間で問題を解くことができ、テストで高得点をとることができます。

　解放パターンを知っていれば簡単だけど、知らないとなかなか気づくことができない問題があるので、解法パターンをある程度知っておくことが大切です。

　ただ、注意しなければならないことは、解法パターンを知っていればそれだけで解けるという問題ばかりではありません。

　解法パターンを使えば簡単に解ける問題も確かにありますが、入試問題では「解法パターン」を考えて応用しなければ解けない問題が多いです。

　解法パターンも基礎と同じく応用するものだということを知っておいてください。

解ける問題の種類を増やす。

　「解法パターン」をたくさん理解していれば、どんな問題も解けることができるというわけではありませんが、理解している「解法パターン」は多いければ多いほどよいです。

　勉強していく上でも、たくさんの問題を解くことを重視して勉強していくのではなく、「解法パターン」をできるだけ多く理解していくことを重視して勉強していくのがよいです。

　大切なのは「どれだけ問題を解いたか」ではなくて、「テストにおいてどれだけ多くの種類の問題を実際に解くことができるか」です。

　テストや入試に出てくる問題にはときどき難問又は奇問が出題されますが、出題されるほとんどの問題は、

　解法パターンをそのまま使って解く問題

　解法パターンを応用して解く問題

　です。

　「たくさんの問題を解く」ことではなく

　「いろいろな種類の問題を解けるようになる」ことにこだわって

　勉強していきましょう。

基礎を応用して問題を解く。

　問題の解き方は覚えるものではありません。

　よく、問題の解き方は覚えるものだと思われているお子様がいますがそれはまちがいです。

　難しい問題の解き方には難しい問題の解き方があるのではありません。

　難しい問題の解き方は、基礎を応用して自分で解き方を考えるものなのです。

　全ての問題は、基礎を応用して論理的に考えれば解くことができるようにできているのです。

　問題の解き方を覚える勉強をしているから、基礎を応用して解く応用問題が解けないのです。

　問題の解き方を覚えようとするのではなく、基礎を応用して自分で解き方を考える勉強をしていきましょう。

思考力を効率よく伸ばしていく。

　数学では、「基礎」と「解法パターン」を応用して論理的に考えて問題を解くことが大切です。

　つまり思考力が鍵になってきます。

　思考力は、どんな頭のいい人も教えることができません。

　思考力は、自分の頭で考えることでしか身につかないものですが、では思考力を効率よく伸ばしていくためにはどうすればいいのか？

　それは、いきなり難しい問題を解こうとするのではなく、

　階段を一段一段上っていくように、段階的に難しい問題を解いていくことです。

　自分の思考力と比べて、自分の考えている内容があまりにも難しすぎると、考えを全く進めることができず、考える力が伸びていきません。

　自分の思考力に合った問題を段階的に解いていき、思考力を効率よく伸ばしていきましょう。

具体的にイメージして考える。

　グラフの問題はグラフ上で。

　平面図の問題は平面図で。

　立体の問題は立体で。

　平面上で、点又は図等が動くなら実際に動くことをイメージして。

　空間で、点又は図等が動くななら実際に動くことをイメージして。

　水槽等に水が入るのなら、水槽を具体的にイメージするとともに入れる水も具体的にイメージする。

　あたり前と言えばあたり前なのですが、そのあたり前のことに気付かないお子様が多いです。

　数字・記号といった文字を中心として考えるのではなく、考えるべきそのものについて具体的にイメージして考えることが大切です。

　頭の中でイメージできる場合は、頭の中で考えればいいですが、もしそうでない場合は具体的にイメージできるよう紙に書いて考えていきましょう。

なぜその解き方をするのか理解する。

　数学で、いろいろな解き方を学ぶと思いますが、なぜその解き方をするのか理解されないお子様がときどきいらっしゃいます。

　中学生の範囲の「代入法」

　高校生の範囲の「漸化式（ぜんかしき）」

　なぜ、その解き方をするのか？

　それは、その解き方が

　「カンタンである。」

　または、

　「その解き方しか解く方法がない。」

　からです。

　どの解き方も、なぜその解き方をするのかつきつめて考えると、その２つの理由に行き着きます。

　もし、本当の意味でなぜその解き方をするのか分かりたければ、ただその解き方を覚えるのではなく、ほかにもっと方法はないかつきつめて考えられてみてください。

　そうすることによって、はじめてその解き方の価値・重要性が分かり、本当の意味で理解したことになるのです。

分かりやすく問題を解くための工夫を考える。

　数学の問題を解くコツは何かというと、分かりやすく問題を解くための工夫を考えて問題を解くということです。

　難しい問題は、自分で分かりやすく問題を解くための工夫をして簡単に解くのです。

　難しい問題になればなるほど、工夫が大切になってきます。

　難しい問題を難しく解いてもいいのですが、それだと解くのにたくさん時間がかかってしまい、またその計算過程も複雑になりミスが起こりやすくなってしまいます。

　分かりやすく問題を解くための工夫の仕方を上達させるには、常日頃、ただ問題を解くだけではなくて、どうすれば簡単に解けるかどうか考えながら、つまり解く過程を重視して問題を解いていくことが大切です。工夫も何も考えずに問題をただ解いていっても、工夫の仕方は上達していきません。

　数学の問題の解き方は、難しい問題になればなるほど、いろいろな解き方で解くことができます。

　ただ解いてよしとするのではなく、

　もっと簡単に解くことはできないか？といろいろな解き方を考えて、

　分かりやすく問題を解くための工夫の仕方を上達させていきましょう。

「もっと良い解き方はないか？」と考える。

　数学は難しい問題になればなるほど、いろいろな解き方で解くことができます。

　そして、一番最初に思いついた問題の解き方が、難しいであった場合、解くのに非常に時間がかかってしまいます。

　最初に思いついた問題の解き方で解くより、考えて簡単な解き方を見つけ簡単な解き方で解いた方が、難しい解き方よりもかなり時間的に短く解くことができます。

　簡単な解き方を見つけれるようになるためにはどうすれば良いか？、

　それは、日頃の勉強において問題を解くことに満足するのではなく、解き方について「もっと良い解き方はないか？」と考え、問題をより簡単に解こうといろいろな解き方を考えてみることです。

　テストのように短い時間でたくさんの問題を解かなければならない場合は別ですが、日頃の勉強においては問題を「解く」ことだけに満足するのではなく、「問題の解き方」にこだわり複数の解き方を考えていきましょう。

　なお、テストの場合においても、問題を解いていく中であんまり複雑でごちゃごちゃした場合は、別の解き方を考えた方が良い場合があります。

　ただし、テストのように限られた時間内でたくさんの問題を解く場合、ある１つの問題において「解き方を考える時間」があまりにも長くなると、そこで「どんなに良い解き方」を考え付いたとしても、テスト全ての問題を解くために必要な時間がなくなってしまいます。

　テストの場合においては、「解き方を考える時間」と「実際に問題を解いていく時間」のバランスに注意しましょう。

「気付く」「見つける」

　数学の問題は、「基礎・解法パターンを応用して論理的に考えて解く」ものであり、その際、「分かりやすく問題を解くための工夫をすることが大切」です。

　しかし、問題を解くための重要な条件に気付いたり、図形問題において、与えられた図等から「問題を解くために必要な条件」を見つけることも重要です。

　これは、「考えること」とは別の脳の働きです。

　「気付く力」「見つける力」は、常日頃、与えられた条件を見て、「問題を解くために重要な条件」を発見したり、分かりやすく問題を解くための工夫をいろいろ考えたりすることによって伸びていきます。

　もう一度言いますが、この「気付く力」「見つける力」は「論理的に考える力」とは全く別の力で、考えることによってではなく、見つけようと意識して問題を見ることでしか伸びていかないものです。

　「考える」だけではなく「気付く」「見つける」ことに意識して問題を解いていきましょう。

問題文に示された条件は全て使う。

　数学においては、問題文に示された条件から、答えを導き出していくのですが、数学において問題文に示された条件は、全て問題を解くために必要な条件だと思ってください。

　つまり、問題文に示された条件は

　問題を解くためのヒント

　だと考えることができます。

　問題が解けないときは、問題文で示された条件の中で使用していない条件がないか確認しましょう。

問題文の条件を解くうえで適切な形に変形

　問題文に示された条件を、別の形に変形して解く場合もあります。

　問題を解くためには、示された条件をどのようにしてとらえるのが良いか？

　ということを考え、

　問題文に示された条件を問題をとくにあたって適切な形に変形し、問題を解きましょう。

問題を解くためには複数の条件が必要

　問題文に示された、１つの条件だけから問題を解くことができることはなかなかありません。

　問題を解くためには、複数の条件が必要な場合が多いです。

　問題を解くにあたって、「複数の問題を解くために必要な条件を見つけ出す」「複数の条件が関係していることに気付く」ことが大切です。

　なお、文章題は「問題を解くために必要な条件」が言葉で示されているのですが、図形問題は言葉で示されていない場合がほとんどです。

「図形問題」においては、「問題を解くために必要な条件」を自分で見つけ出しましょう。

必要な条件を「見つけ出す」「導き出す」

　図形問題に多いのですが、問題を解くために必要な条件が、問題文に示されていない場合があります。

　そういった場合には、問題文に示された条件を、与えられた条件から「導き出す」ことが必要になってきたり、「見つけ出す」ことをしなければなりません。

　ここで注意しておいて欲しいのが、記述問題において問題文に示されていない条件を見つけ出した場合、その条件が正しく成り立つということを証明してから問題を解くのにその条件を利用していくことです。

　そうでないと、本当にその条件が正しくても、解答においてその条件は「正しい条件」ではなく「ただ正しいと思っている条件」ということになってしまうからです。

大問の（１）（２）の答えは（３）のヒント

　数学の大問で（１）（２）（３）と順々に解いていく問題において、

　（１）の答えは、（２）を解くためのヒント

　であり

　（１）（２）の答えは（３）を解くためのヒント

　である場合があります。

　（２）（３）を解く場合は、「問題文に示された条件」や「公式」「解法パターン」だけではなく、

　（１）（２）の答えも「問題を解くために使う条件」、つまり「問題を解くためのヒント」と考えて解いていくことが大事です。

　どんな問題においても、視野を広くして「問題文に示された条件」「公式」「解法パターン」「前の問題の答え」をよく見渡し、どれを使えば目の前の問題を簡単に解くことができるか考えることが大事です。

何が分かれば分かるのか？

　数学において、問題を解くための条件が足りないとき、「何が分かれば分かるのか？」と自問自答することが有効です。

　そして「分からなければならないもの」が分かったのなら、それを求めればいいのです。

要するにどういうことなのか？

　「要するにどういうことなのか？」という問いかけることによって、問題文に示された複雑な条件を簡単なものに言い換えることができたり、複数の複雑な条件を頭の中で一気にまとめあげることができる場合もあります。

　問題文に複雑な条件が示されている場合は「要するにどういうことなのか？」と考えてみましょう。

もっとカンタンな解き方はないか？

　数学は難しい問題になればなるほど、いろいろな解き方で解くことができます。

　難しい問題を解く場合、一番最初に思いついた問題の解き方でそのまま解こうとするのではなく、

　もっとカンタンな解き方はないか？

　と、問いかけ考え、

　「カンタンな解き方」を考え出す、見つけ出すようにしましょう。

　「カンタンな解き方」を考え出す、見つけ出し、その「カンタンな解き方」で解いた方が、最初に思いついた問題の解き方で解くより、時間的に短く解くことができます。

　ある解き方では解くのに３０分かかる問題でも、

　「カンタンな解き方」で解けば５分で解ける場合もあります。

　テストは時間勝負です。

　できるだけ「カンタンな解き方」で解くようにしましょう。

計算問題を解くコツ

　計算問題を解くコツは、カンタンに計算するための工夫をすることです。

　足す順番を変える。

　かける順番を変える。

　計算の順番を変える。

　まとめ方を変える。

　式の部分部分を見るのではなく、式全体をみわたして、どのように計算を工夫すれば簡単にできるか考えることです。

　計算問題を解くコツは、

　ただ普通に何も考えずに計算していくのではなく、

　式全体を見渡して、どのように工夫すれば簡単に計算できるかを考えて計算することです。

文章題を解くコツ

　基本は、問題文に書いてあることを式にすることです。

　問題文に書いてあることを式にしにくい場合は、

　１度、文章に書いてあることを図にして、その図から式をつくってください。

　また、問題文から複数の式を作ることがあります。

　その場合は、「式を作ることのできる文」を見つけなければなりません。

　連立方程式の文章題などがそれです。

　連立方程式の文章題は「式を作ることの出来る文」が２つあります。

　その２つの文を見つけて、式を作って解きます。

　問題文に書いてあることを式にする。

　式にしにくい場合は図にしてから式をつくる。

　いくつかの式を作る場合は、式を作ることのできる文を見つける。

　この３つが文章題を解くコツです。

図形問題を解くコツ

　図形問題を解くコツは、

　図に書かれていない

　「図から明らかにすることができる全ての条件」を

　「見つける」「気付く」

　それから、解き始めることです。

　図形問題は、「問題を解くために必要な条件」が見つからなければ絶対に解けません。

　その「問題を解くために必要な条件」は、「図から明らかにすることができる全ての条件」にふくまれています。

　まずは、「図から明らかにすることができる全ての条件」を見つけましょう。

点・図が動く問題を解くコツ

　点・図が動く問題を解く場合は、実際に動いた図を書いてみましょう。

　書く図の数は、問題によって２つだったり、３つだったり、４つだったりします。

　実際に、点・図が動く問題をいろいろ解いていけば、書く図の数は自然に分かってくると思います。

　点・図が動く問題を解く場合は、

　問題文に書かれた動いていない図を見るのではなく

　実際に動いた図を書いて、

　それから考えましょう

証明問題を解くコツ

　証明問題は、

　証明の過程（かてい）

　が解答になります。

　証明問題を解くコツは、

　「証明の過程を書きながら考える」

　のではなく

　「証明の過程が最初から最後まで分かってから、解答に証明の過程を書く」

　ことです。

　「証明の過程」を書くのは、証明の過程が最初から最後まで分かってからです。

　それはなぜか？

　それは、書きながら考える場合、

　書くのにも時間がかかりますし、

　書きながら考えててもし途中で、その考えている道筋では証明できないと分かったら、

　結局その書いた部分がムダになってしまうからです。

　まずは、証明の過程を最初から最後まで分かること。

　それから、解答に証明の過程を書きましょう。

　ただし、証明の過程が最初から最後まで分からない場合もあると思います。

　その場合は、

　部分点をもらうために、

　証明できない過程を解答に書けるところまで書きましょう。

規則性の問題を解くコツ

　規則性を「見つける」「気付く」ことです。

　ただ、それだけです。

　「見つける」「気付く」というのは、「考える」「計算する」「式を作る」とは別の頭の使い方です。

　規則性の問題は考えようとしないことです。

　考えても規則性は見つかりません。

　規則性を見つけよう

　規則性に気付くこう

　そのように思いながら、問題を解いてください。

問題を解く過程の美しさにこだわる。

　数学を得意になりたいと思ったら、

　問題が正解したことに喜ぶのではなく、

　問題をカンタンに解くことに喜びを感じることです。

　カンタンな解き方

　つまり

　問題を解く過程の美しさにこだわることです。

　正解することにこだわるのではなく

　問題を解く過程の美しさにこだわりましょう。

数学はイメージが大切

　計算問題は計算力があれば解くことができます。

　しかし、「文章で書かれた問題」や「図形の問題」は想像力がなければ解くことができません。

　想像力とは「実際に見えない物事について、具体的に頭の中でイメージする力」のことです。

　紙に書かれた平面図形・立体図形を頭の中で「イメージする力」、文章で書かれた問題を読んでその文章に書かれている内容を「イメージする力」のことです。

　「文章の問題」「図形の問題」が苦手な子は、想像力がないから、つまり頭の中で考えるべき内容を「イメージする力」ないから苦手なのです。

　では、想像力つまり「イメージする力」を身につけるにはどうすればよいのでしょうか？

　それは、「問題文に書かれている内容」「平面図形」「立体図形」を、頭の中ではっきりと映像として映し出してみることです。

　「思い出」を思い出すのを考えてみてください。思い出を思い出すとき、その思い出ははっきりと映像として見えているるはずです。それと同じことをするのです。

　思い出を映像として見ることができるのなら、イメージすることもできるはずです。

　数学は、思い出を映像として見るのと同じように「イメージ」するようにしましょう。

分かっていないことで１番基礎的な内容を勉強

　難しい問題ができない理由。

　それは、基礎ができていないからです。

　どのお子様も、そのお子様がするべき最善の勉強は

　「分かっていないことで１番基礎的な内容」を勉強することです。

　それが、最善です。

　つまり、それ以外の勉強は最善でないということです。

　「自分にとって最善の勉強は何か？」を考えて勉強しましょう。

論理的かつ数学的に考える。

　「論理的に考える」とは

　「根拠に基づいて結論を導き出す」

　ということです。

　そして、「論理的・数学的に考える」とは

　「数学のルールにしたがって根拠に基づいて結論を導き出す」

　ということです。

　数学ができないお子様にありがちなのは

　「数学のルールではなく自分のルールにしたがって根拠に基づいて結論を導き出す」

　ことです。

　数学は、何のルールもなしに自分なりに自由に考えるものではありません。

　数学のルール（決まり）の範囲の中で、考えていくものです。

　論理的かつ数学的に考えましょう。

　なお、数学が苦手なお子様の中には、

　「１つのルールなら守って考えることができるけど、ルールの数が４つ・５つになるとルールを守って考えることができない」

　というお子様が多いような気がします。

　１つのルールにだけ注意をするのではなく、全てのルールを守るようにしましょう。

計算のコツ

　計算のコツの一覧です。

　リンクをクリックするとコツの内容が表示されます。

　・ 順番を変え上手に組み合わせる。

　・ 分けて上手に組み合わせる。

　・ よく出る変換・計算を暗記しておく。

　・ 公式の活用に気付く。

　・ 基準となる数をつくり計算を工夫する。

　・ 計算しやすいように置きかえる。

　・ 掛け算・割り算の混じった計算は分数に。

　・ 「少数の掛け算・割り算」は分数に。

　・ 約分は早めにする。

　・ 「同じもの」「仲間どうし」をまとめる。

　・ 計算結果の変わらない計算を付け加える。

　・ 問題を変換する。

　・ イメージされる答えから計算方法を決める。

　・ 数学的に考えて計算する。

　・ つまり「計算問題を解くコツ」とは？

順番を変え上手に組み合わせる。

１　足し算・引き算

    33+45+67=（33+67）+55=100+45

    22+45+28=（22+28）+45=50+45

    30+67-27=（30-27）+67=3+67

    55-20-49=（55-49）-20=6-20　　

２　掛け算・割り算

    25×21×4=25×4×21=100×21=2100

    8×13×125=（8×125）×13=1000×13

    4×4×4×25×25×25=（4×25）×（4×25）×（4×25）=100×100×100

    16×5÷2=（16÷2）×5=8×5

    3.54×0.9÷0.45=3.54×（0.9÷0.45）＝3.54×2

分けて上手に組み合わせる。

１　足し算・引き算

    48+16=48+（2+14）=（48+2）+14=50+14

    579+175=(579+21)+(175-21)=700+154=854

    36+88=（24+12）+88=24+（12+88）=24+100=124

    46+18=（44+2）+18=44+(2+18)=44+20=64

    1690-298=（1390+300）-298=1390+(300-298)=1390+2=1392

    4297-1075=（4200+97）-（1000+75）=（4200-1000）+（97-75）=3200+22

    53093-27744=23000+30000-27700+93-44=23000+2300+49

    1443-675=（700+743）-675=（700-675）+743=25+743

２　掛け算・割り算

　　42×25=21×2×25=21×50=1050

　　65×16=65×4×4=260×4=1040

　　64×45=32×2×45=32×90=2880

　　240÷16=240÷4÷4=60÷4=15

　　1260÷18=1260÷6÷3=210÷3=70

　　540÷45=540÷9÷5=60÷5=12

よく出る変換・計算を暗記しておく。

１　よく使う「少数から分数への変換」

２　よく出る「２乗の計算」

公式の活用に気付く。

１　a×（b+c）＝ab+ac　（a+b)×c＝ac+bc

　　 190×210=(200-10）（200+10）=40000-100

基準となる数をつくり計算を工夫する。

　　52+55+57+46+49+41
　　=（52-50)+(55-50)+(57-50)+(46-50)+(49-50)+(41-50)+50×6
　　=2+5+7-4-1-9-6+50×6

　　800-197×4=200×4-197×4=(200-197)×4

　　1000-188×5=200×5-188×5=(200-188×5=12×5

　　1590-398×4=290+400×4-398×4=290+（400-398）×4=290＋8

計算しやすいように置き換える。

掛け算・割り算の混じった計算は分数に。

「少数の掛け算・割り算」は分数に。

約分は早めにする。

「同じもの」「仲間どうし」をまとめる。

１　同じ数をまとめる。

　　60-7-7-7-7=60-4×7

２　足し算、引き算をまとめる。

　　35+3273-1511+10669-4633=(35+3273+10669)-(1511+4633)

３　「同じ掛け算をふくむもの」どうしをまとめる。

　　14×29-19×13+21×14+15×19=14×(29+21)+19×(15-13）

　　1.35×33＋305×1.35-157×1.35=2.37×（33+305-157）

計算結果の変わらない計算を付け加える。

１　５の倍数を掛けるとき「÷2×2」「÷4×4」「÷8×8」などを付け加える。

　　3056×5=3056÷2×2×5=1528×10

　　287×5=287÷2×2×5=143.5×10

　　56×15=56÷2×2×15=28×30

　　28×25=28÷4×4×25=7×100

　　56×125=56÷8×8×125=7×100

２　５の倍数で割るとき「×2÷2」「×4÷4」「×8÷8」などを付け加える。

　　231÷5=231×2÷2÷5＝462÷10

　　261÷15＝261×2÷2÷15=522÷30

　　412÷25=412×4÷4÷25=1648÷100

　　2800÷125=2800×8÷8÷125=24000÷1000

問題を変換する。

　1000-897

　897にたして1000になる数は？

　5-1.33

　1.33にたして5になる数は？

　600-428

　428にたして600になる数は？

イメージされる答えから計算方法を決める。

数学的に考えて計算する。

　　ある２つの数が「ある同じ公約数」を含む場合、

　　その２つの数の差は「ある同じ公約数」を含む。

　（活用例その１）

　（活用例その２）　　

関数の問題

　１次関数、２次関数などの「関数の問題」は

　方程式として式として考えるのではなく、「xy平面」における「図」として考えましょう。

　「xy平面においてどういう図になっているか？」ということが

　しっかりイメージできることが大切です。

　もし、頭の中でイメージできないのであれば、実際に「xy平面」にグラフを書いて考えましょう。

１番いい解き方を考える。

　数学において「考える」ということは

　「１番いい解き方を考える」ということです。

　問題を解くことにこだわるのではなく、

　問題の解き方にこだわりましょう。

読書をして読解力を身につける。

　読解力といえば、国語の問題を解くために必要なものであり、数学には関係ないと思われる方がいるかもしれませんが、数学においても読解力は必要不可欠です。

　必要な理由は２つあります。

　１つは、読解力がなければ教科書や参考書に書いている内容が理解できません。

　もう１つは、読解力がなければ問題文を理解できず、問題を解くことができません。

　読解力は、自分の好きな活字の本を常日頃読んでいれば自然に身につきます。

　「ライトノベル」が好きであれば、「ライトノベル」でもＯＫです。

　読書をして、読解力を身につけましょう。

つまらない勉強をしない。

　算数・数学においてつまらない勉強とは、

　「同じような問題を繰り返し解くこと」

　です。

　小学生は、「算数のドリル」を必ずすると思います。

　「ドリル」とは、英語で「訓練」の意味ですが、「算数のドリル」で同じような問題を繰り返し解かせる「訓練」のような算数の勉強をさせるから、子どもが算数嫌いになるのです。

　算数・数学のおもしろさとは、

　「見たことがない問題を解くこと」

　「もっとエレガントな解き方はないかと考えること」

　にあります。

　「訓練」のような、算数・数学の勉強はなるべくしないようにしましょう。